Hybridizing intra and extra perspectives in infectious disease modeling

The last four decades have been particularly marked by devastating diseases. During this period, humanity has experienced plagues such as SARS, bird Flu, Ebola, Chikun-gunya, COVID-19 in addition to diseases that were already decimating populations.

Health agents have set to work fighting these scourges by putting their own lives in danger. Their work has been remarkably supported by researchers in Mathematics and Computer Science in the sense that, when an effective cure for a disease lacks, measures could be taken to minimize its spread. Recently, equation-based models (from Mathematics) and agent-based models (from Computer Science) have proven effective in the fight against infectious diseases.

However, there are two points of view when one deals with the dynamics of a disease spread: the first point of view concerns the disease evolution in the host organism (intra) and the second one concerns its evolution in the population (extra). In many scientific publications, the two aspects are studied separately even if they contribute to the understanding of the same phenomenon.

Since the seminal work of Ross in the 1910s and of MacKendrick in the 1920s-1930s, different mathematical models have been proposed both in the intra and extra context.

The first model used in epidemiology that described smallpox infection was published in 1766 by Daniel Bernoulli [1]. It was the first time that the whole epidemiological observations on smallpox were collected, combined with demographic data of that time, and inserted into a mathe-matical model in order to verify hypotheses and to assess the cost-benefit ratio of variolation (preventive inoculation of smallpox for immunization of the subject) [2].

In the continuation of the above-mentioned work, several other researchers have contributed to the study of infectious disease dynamics. In [3], a SEIAR (Susceptible-Exposed-Infectious-Asymptomatic-Recovered) model is compared to an agent-based one to understand the dynamics of COVID-19 spread. A SEIRD (Susceptible-Exposed-Infected-Recovered-Deceased) with three forms of infection (benign, respiratory, and severe forms) is presented in [4]. Other mathematical models to control the spread of infectious diseases are studied in [5-15].

The remainder of the paper is organized as follows: First, I define some key concepts (Section 2), then I suggest a novel approach to study the spread of infectious diseases (Section 3). Finally, I conclude the study and give some recommendations for future works (Sections 4,5).

Basic terminology

Model: A model is a representation of a reality obtained by retaining only the aspects essential to its understanding. It is a reality simplified representation. Thus, a model is never an exact reproduction of reality but rather its clarified and purified image. A model always relates to what one hopes to deduce from it. Different models may refer to the same object depending on what one is interested in. Modeling is the action of constructing a model.

Equation-Based Model (EBM): An EBM is a model consisting of mathematical equations (generally differential equations). One must evaluate these equations to execute the model.

Most mathematical models are built on EBMs. Particularly in epidemiology, it has been shown that in case of a lack of a cure for an infectious disease, certain measures should be taken to mitigate the damage. Mathematical models supported by computer simulations allow for determining the factors that most influence the spread of disease. Thus, such an approach can help to decide on one measure rather than another to fight against the disease.

Among such models, we can mention SI, SIS, SIR, SEIR, SEIRS, SEIRD, etc. This approach provides an analysis of the model’s pure mathematical characteristics such as the positivity of the solution, the uniqueness of the solution, the endemic and the disease-free equilibria, the stability of equilibrium points, and the basic number of reproduction [3].

Agent-Based Model (ABM): ABMs derive from artificial intelligence, essentially from multi-agent systems (MAS). Such models allow the description of each agent’s behavior using an algorithm [5]. They are more precise and very close to reality. Biologists, mathematicians, and computer scientist’s work together to develop high-tech tools in order to simulate models for infectious diseases spread [16].

Intra modeling: In epidemiology, an intra-model is a representation of the evolution of a disease in the host organism. Most diseases do not show up immediately. They need an incubation time to make the host sick. Even during the incubation period, some of them are often transmitted from person to person. Hence the need to take this reality into account in the model.

Extra modeling: An extra model concerns the way a disease spreads in the population. Compartmental models study the different states of this evolution (compartments of susceptible, exposed, infected, asymptomatic, recovered, quarantined, deceased, etc.).

Combining intra and extra models

In this paper, I advocate the hybridization of intra and extra points of view when dealing with infectious disease spread. Such an approach has already been used to study the dynamics of malaria and TB spread [17,18]. Proceeding in this way would make it possible to take into account, in the model, the incubation period of the disease as well as the other parameters, both endogenous and exogenous.

For example, the cure and the quarantine could be combined to study both intra and extra-disease evolution.

In [17] a rigorous mathematical analysis is given along with the basic reproduction number (R0) for TB dynamics control in DRC. The study shows that loss to follow-up and transferred people constitute a risk, but still less than germ-carrying cases. Latent/exposed rapidly evolving cases are responsible for the increase in incidence in the short and medium term, while the evolution of latent/exposed cases will be responsible for the long-term persistence of the incidence and maintenance of tuberculosis and to delay elimination in the population. Finally, the authors prescribe contact monitoring, detection of latent people, and treatment to control TB in the population.

An EBM is presented in [18] to model the spread of malaria in human and mosquito populations. Authors find that the disease-free equilibrium is locally asymptotically stable when the basic reproduction number is less than 1 and unstable when R0 > 1.

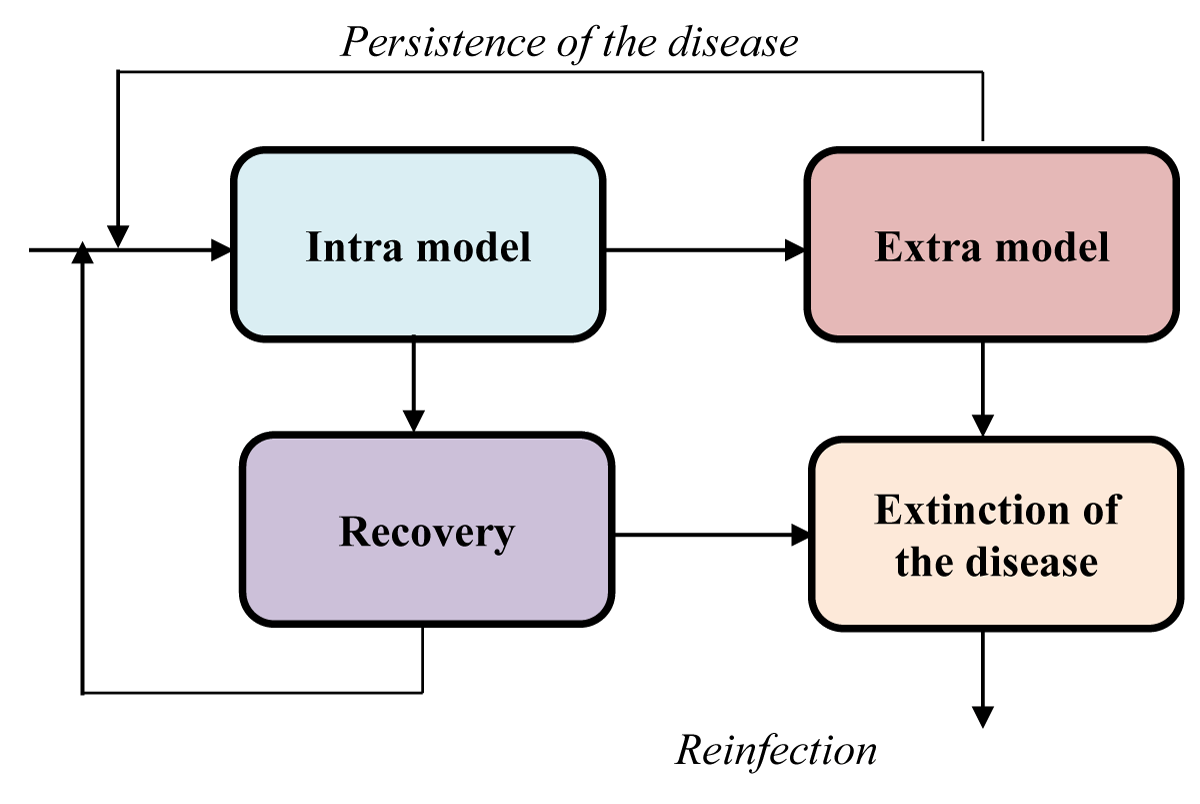
In Figure 1 below, I propose a model to study infectious disease spread phenomena. Intra and extra models are to be placed in the places indicated in the suggested model.

In this article, I advocate the combination of intra and extra-modeling to study the spread of infectious diseases. Such a representation is more realistic than those that have chosen to study the problem using a single point of view.

Hybridizing intra and extra points of view allows for dealing with a complex and realistic model taking into account endogenous and exogenous parameters. Then, ABM or EBM can be used solely or combined to build the entire model.

Future works

The greatest challenge in an epidemiological study is to combine these two approaches (intra and extra) in modeling an epidemic such as Ebola, Cholera, or even COVID-19. It will be a question of adequately placing the intra and the indicated places while considering that the entry to the intra phase is consecutive to the infection. Thus, susceptible (S), exposed (E), and infected (I) compartments, if they have to be considered in the model, will be placed before the intra-phase.

1. Bernoulli D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir. Histoire de l’Académie royale des sciences: mémoires de mathématiques et de physique. 1766; 1–40.
2. Valleron AJ. Les rôles de la modélisation en épidémiologie. Comptes rendus de l’Académie des sciences. Série III, Sciences de la vie. 2000; 323: 5:429-433.
3. Kasereka SK, Zohinga GN, Kiketa VM, Ngoie RBM, Mputu EK, Kasoro NM, Kyandoghere K. Equation-Based Modeling vs. Agent-Based Modeling with Applications to the Spread of COVID-19 Outbreak. Mathematics. 2023; 11:253. https://doi.org/10.3390/math11010253
4. Ndondo AM, Kasereka SK, Bisuta SF, Kyamakya K, Doungmo EFG, Ngoie RBM. Analysis, modeling and optimal control of COVID-19 outbreak with three forms of infection in the Democratic Republic of the Congo. Results Phys 2021; 24:104096.
5. Kasereka S, Kasoro N, Chokki AP. A hybrid model for modeling the spread of epidemics: Theory and simulation, in. In: SKO-Maghreb: Concepts and Tools for knowledge Management (ISKO-Maghreb). 2014 4th International Symposium. IEEE; 2014; 1-7.
6. Kasereka S, Le Strat Y, Léon L. Estimation of infection force of hepatitis c virus among drug users in france. In: Recent Advances in Nonlinear Dynamics and Synchronization. Springer. 2018; 319-344.
7. Ndondo A, Munganga J, Mwambakana J, Saad-Roy C, Van den Driessche P, Walo R. Analysis of a model of gambiense sleeping sickness in humans and cattle. J Biological Dyn. 2016: 10:347-65.
8. Goufo EFD, Maritz R, Munganga J. Some properties of the kermack-mckendrick epidemic model with fractional derivative and nonlinear incidence. Adv Diff Eq. 2014; 2014:278.
9. Ndondo AM, Walo RO, Vala-Kisisa MY. Optimal control of a model of gambiense sleeping sickness in humans and cattle, American. J Appl Math. 2016: 4:204-216.
10. Kasereka S, Goufo EFD, Tuong VH. Analysis and simulation of a mathematical model of tuberculosis transmission in democratic republic of the congo. Adv Diff Eq. 2020: 642:1-19.
11. Kasereka S, Goufo EFD, Tuong VH, Kyamakya K. A stochastic agent-based model and simulation for controlling the spread of tuberculosis in a mixed population structure. In: Developments of Artificial Intelligence Technologies in Computation and Robotics, Prodeedings of the 14th International FLINS Conference (FLINS 2020), Cologne, Germany, 188-21 August 2020, World Scientific, 2020; 659-666.
12. Redhwan SS, Abdo MS, Shah K, Abdeljawad T, Dawood S, Abdo HA, Shaikh SL. Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator. Results Phys. 2020; 19:103610.
13. Din RU, Shah K, Ahmad I, Abdeljawad T. Study of transmission dynamics of novel COVID-19 by using mathematical model. Adv Diff Eq. 2020; 2020: 1-13.
14. Zhang Z, Zeb A, Hussain S, Alzahrani E. Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv Diff Eq. 2020; 2020: 1-12.
15. Din RU, Seadawy AR, Shah K, Ullah A, Baleanu D. Study of global dynamics of COVID-19 via a new mathematical model. Results Phys. 2020; 19:103468.
16. Tracy M, Cerdá M, Keyes KM. Agent based modeling in public health: Current applications and future directions. Annu Rev Public Health. 2018; 39:77-94.
17. Kasereka S, Goufo EFD, Tuong VH. Analysis and simulation of a mathematical model of tuberculosis transmission in democratic republic of the congo. Adv Diff Eq. 2020: 642:1-19.
18. Chitnis N, Cushing JM, Hyman JM. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J Appl Math. 2006; 67:24-25.